Introduction
Peanut drying reduces the moisture content (MC) of harvested peanuts to a level at which the quality is maintained (Young et al., 1982). Drying is generally performed in two stages: 1) field curing in inverted windrows to 20–25% dry basis MC, and 2) drying in wagons or bins to about 10% dry basis MC (Baldwin et al., 1990).
Field curing is a natural process and the factors that affect it have been studied and described extensively by other researchers (Young et al., 1982). Wagon or bin drying is a process in which water is removed from farmer stock peanuts (field dried peanuts at 20–25% MC dry basis) through moisture and temperature gradients created by air flowing through the mass of peanuts. In practice, the wagon contains a deep bed of peanuts, where air is forced upwards through the peanuts. Requirements for air flow in terms of volume, temperature and relative humidity, in wagon drying, combined with the drying time (about 18–24 h), make drying in wagons an energy intensive process. A large number of studies have been conducted to determine ways to increase the energy efficiency in air drying of peanuts (Troeger, 1982; Blankenship and Chew, 1978; Rogers and Brusewitz, 1977; Chai and Young, 1995). Past studies have frequently focused on the use of high temperatures and methods of reducing the amount of running time for fans (Baker et al., 1993; Blankenship and Chew, 1979; Butts, 1996).
Little research has been conducted on the use of alternative methods for energy input, such as microwave or radio frequency energy. The microwave region of the electromagnetic spectrum has long been used in a variety of industrial applications, ranging from telecommunication to dielectric heating of foods and other materials. Due to the large number of applications available, the Federal Communication Commission (FCC) regulates the use of the frequency bands of the electromagnetic spectrum, and the two microwave frequencies reserved for dielectric heating in the United States are 915 and 2450 MHz. The mechanism of dielectric heating has been thoroughly analyzed and described in many studies (von Hippel, 1954; Rosenthal, 1992; Clark et al., 1997; Schiffmann, 1997).
The potential for ionic conduction and dipole rotation of materials is expressed by the imaginary part of the relative complex permittivity (relative dielectric loss) (Nelson, 1973; Boldor, 2003):
 1
1
-
ϵ* - relative complex permittivity or relative complex dielectric constant; -
-
ϵ′ - relative electric constant or storage factor; -
-
ϵ″ - relative dielectric loss or loss factor; -
-
j – (−1)1/2 - imaginary part of a complex number
The power dissipated in dielectric heating is proportional to the frequency, dielectric properties and the electric field distribution according to the formula (Nelson, 1973; Metaxa and Meredith, 1983):
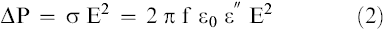 2
2
-
ΔP - power absorbed per unit volume; W/m3
-
σ - conductivity; siemen/m
-
E - electric field; V/m
-
f - frequency; Hz
-
ϵ0 - dielectric constant of the vacuum = 8.854 10−12 Far/m
Microwave heating has been used in the past to reduce the MC of various fruits and vegetables such as banana (Musa acuminate), (Maskan, 2000); apples (Malus pumila) ; mushrooms (Amanita aspera); and strawberries (Aphelenchoides fragariae), (Funebo and Ohlsson, 1999; Funebo et al., 2000; Erle and Schubert, 2001); carrot (Daucus carota), (Prabhanjan et al., 1995; Sanga et al., 2000); corn (Zea mays L.), (Shivhare et al., 1991; Beke et al., 1995; 1997); potatoes (Solanum tubersum), (Bouraoui et al., 1994; Sanga et al., 2000); and broad beans (Phaseolus vulgaris), (Ptasznik et al., 1990). Blanching of endive (Chicorum endiva) and spinach (Spinacia oleracea), (Ponne et al., 1994), corn, (Boyes et al., 1997), and peanuts (Arachis hypogaea L.) (Rausch, 2002) as well as studies performed to investigate the shelf life and roast quality of microwave blanched peanuts (Katz, 2002) are also examples of utilization of microwave energy in processing of foods and agricultural commodities. Most of these studies were performed on static samples that were not characteristic of an industrial environment typified by continuous processing. With a few exceptions (Rausch, 2002; Katz, 2002), the referenced studies were based on modifications of multimode cavity home microwave ovens to allow air flow and temperature and mass measurement. An inherent problem in the use of multimode cavity ovens is non-uniform heating due to standing wave patterns created by the electric field (Rosenthal, 1992). Another drawback is that the multimode cavity home-oven frequency (2450 MHz) yields a shorter wavelength than the 915 MHz frequency found in industrial applications and therefore a shorter penetration depth (Metaxa and Meredith, 1983).
The TE10 (transverse electric) traveling mode applicators for drying are widely used in the wood and paper industries (Metaxa and Meredith, 1983; Jones, 1975; Jones, 1986). The distribution of the electric field is relatively uniform at the center of any transversal section perpendicular on the main axis of a TE10 waveguide (Boldor et al., 2005). A dielectric material placed at the center of the waveguide, running parallel with the electrical field, will be heated uniformly by the electric field.
The typical temperature profile and electric field distribution in continuous microwave drying of peanuts are described in another study (Boldor, 2003). Along the longitudinal axis of the waveguide, the electric field decreases exponentially as a function of distance, while the temperature profiles have three distinct regions (Boldor, 2003; Roussy and Pierce, 1995; Metaxa and Meredith, 1983). Initial heat-up occurs in the first region. The second region is the constant temperature drying region, and the third region is a region of temperature increase without any drying. For all practical purposes, any microwave drying process should stop at the end of the constant temperature drying region to maintain product quality.
This study focused on the effect of microwave power level and peanut initial MC on temperature distribution and potential for moisture removal of farmer stock peanuts (25 to 45% MC dry basis) in a continuous TE10 traveling wave applicator using 915 MHz microwaves.
The general governing equation for the transport phenomena assuming negligible radiating losses during microwave drying is (Boldor et al., 2005, Metaxa and Meredith, 1983; Lu et al., 1999):
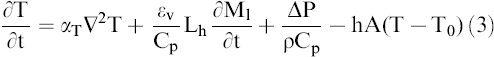 3
3
-
T - temperature; K, °C
-
T0 - ambient temperature; K, °C
-
t - time; s
-
αT - thermal diffusivity; m2/s
-
ϵv - ratio of vapor flow to total moisture flow; -
-
Cp - specific heat; J/kg K
-
Lh - latent heat of vaporization; J/kg
-
Ml, - moisture content (liquid); % db
-
ρ - bulk density; kg/m3
-
h - convective heat transfer coefficient; W/m2 K
-
A - surface area of a peanut pod; m2
The coupling between heat and mass transfer phenomena described by Equation [3] makes analytical solution extremely difficult. Boldor et al. (2005) used the unique properties of the traveling wave applicators and assumptions to simplify the equation and divide the waveguide into the two regions. In the first region moisture loss and temperature gradient were considered negligible due to the volumetric heating and Equation [3] was reduced to (Boldor et al., 2005):
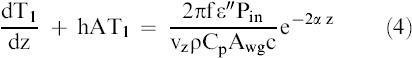 4
4
-
T1 = T – T0; K, °C
-
Pin - power input into the system; W
-
vz - belt speed; m/s
-
Awg - cross sectional area of the waveguide; m2
-
c - speed of light; 3×108 m/s
-
α - attenuation constant; m-1, dB/m
-
z - distance coordinate; m
In the second region, only drying at a constant temperature occurs and Equation [3] reduces to (Boldor et al., 2005):
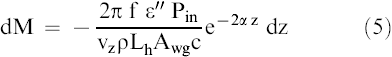 5
5
-
M - moisture content; % db
The solutions to Equations [4] and [5] and the discussion of the effect of moisture dependence on dielectric loss are presented elsewhere (Boldor et al., 2004; 2005).
Materials and Methods
Runner- and virginia-type peanuts were partially dried in windrows to MCS ranging from 25 to 45% dry basis. Samples were shipped from the USDA, ARS National Peanut Research Laboratory in Dawson, Georgia to the Department of Food Science at North Carolina State University during the months of September to November of 2002.
The microwave curing chamber (Industrial Microwave Systems, Morrisville, NC) was a traveling wave applicator composed of a conveyor belt running (vz = 8.4 mm/s) at the geometrical center along the axis of an aluminum waveguide. The microwaves were generated by a 5 kW microwave generator (Industrial Microwave Systems, Morrisville, NC) and transported to the curing chamber through aluminum waveguides. The curing chamber was outfitted with an electric fan and an electric heater to assist the microwave drying process. The heater was set to maintain an ambient temperature of 25 C in the chamber. The microwave generator was controlled through a data acquisition and control unit (HP34970A, Agilent, Palo Alto, CA) and a software routine written in LabView (National Instruments Corp., Austin, TX). The data acquisition unit and the software monitored and recorded the power output, reflected power and power at the exit of the microwave curing chamber through power diodes (JWF 50D-030+, JFW Industries, Inc., Indianapolis, IN).
All temperature measurements during microwave curing were performed using fiber optic probes and remote infrared temperature measurement (Mullin and Bows, 1993; Goedeken et al., 1991). The fiber optic probes (FOT-L/ 10M, Fiso Technologies, Inc., Quebec, Canada) were connected to a multi-channel fiber-optic signal conditioner (Model UMI 4, Fiso Technologies, Quebec, Canada) remotely controlled by FISOCommander software (FISO Technologies, Quebec, Canada) installed on a laptop computer (Dell Inspiron 8500, Dell Computer Corp., Round Rock, TX). The surface temperature of the peanut bed (3 cm thick) was monitored with infrared thermocouples (model OS36-T, OMEGA Engineering, Inc., Stamford, CN) placed at various distances along the waveguide. The surface temperatures were monitored and recorded using the same software routine that was used to control the generator and to record the power levels.
A Thermovision Alert N infrared camera (FLIR Systems AB, Danderyd, Sweden) was placed at the exit of the microwave curing chamber to monitor the spatial temperature distribution of the peanut bed surface. The camera was controlled by Thermovision Remote software (FLIR Systems AB, Danderyd, Sweden) installed on a laptop computer (Samsung SensPro 520, Samsung, Ridgefield Park, NJ).
Data collection was started simultaneously for all three systems (fiber optic probes, infrared thermocouples and infrared camera) in order to match the temperature measured with the fiber optic probes with the surface temperatures of the peanut bed as measured by the infrared thermocouples and the infrared camera.
Data were collected based on two experimental designs. The first reused the same samples (both runner- and virginia-type peanuts) in three consecutive passes at two power levels (1.2 and 2 kW) to simulate a three-stage microwave curing chamber.
For one sample of runner-type peanuts with an initial MC of 29%, the fiber optic probes were mounted such that both the internal temperature of the seed and the temperature at the pod surface were monitored while in the microwave curing chamber. For the other samples (one runner-type of 25% initial MC and one virginia-type of 46% initial MC), only the internal seed temperatures were monitored with fiber optic probes in the microwave curing chamber.
The second experimental design used runner-type peanuts to study the effect of six power levels (0.3, 0.6, 0.9, 1.2, 1.5, and 2 kW) and four initial MCs (33, 21, 14, and 11%) on seed temperatures, heating rates and MC. In order to get starting material of desired initial MCs, peanuts were dried with ambient air.
The power levels denoted in this paper were set points on the control panel of the software routine. Due to the non-linearity of the data acquisition and control unit, the nominal power levels (or the power output) of the generator were always smaller than the set points. The reflected power was caused by the change of impedance of the waveguide where the microwaves entered the planar applicator (Stuchly and Hamid, 1972; Griffiths, 1999). Although the impedance mismatch was minimized through the special design of the waveguide connector, the reflected power was considered lost.
The internal temperature measurements were performed on 8 to 12 peanut pods in two replicates. The fiber optic probes were placed in pods in previously drilled holes and spread to cover the whole width of the conveyor belt.
For each set of data the temperature profiles along the waveguides were determined by averaging all the measurements from the two replicates for the fiber optic probes measurements (internal temperatures) and the infrared thermocouple measurements (surface temperatures). Bulk MCs of the samples was determined using the ASAE standard (ASAE, 2000).
All temperature and MC data, with the exception of the infrared images, were processed using Microsoft Excel 97 (Microsoft Corp, Redmond, WA). The data on the spatial distribution of temperatures in the temperature images acquired with the infrared camera were processed with the Thermacam Researcher software package (FLIR Systems AB, Danderyd, Sweden).
Results and Discussion
Experimental Design 1
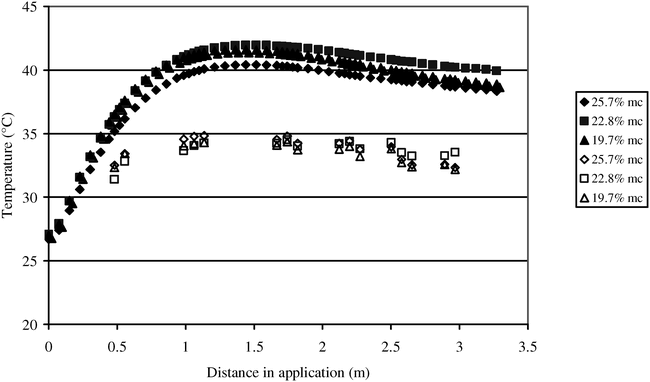
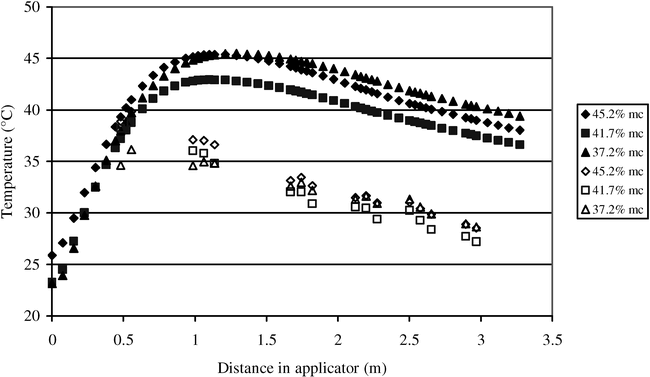
Examples of internal temperature profiles in the microwave curing chambers for the consecutive passes of virginia- and runner-type peanuts at power levels of 1.2 and 2 kW are presented in Fig. 1 and 2. The difference between the temperature profiles was negligible in the three consecutive passes (different initial MCs) at the same power level. This behavior is consistent with theoretical models previously developed (Boldor et al., 2005). After reaching a maximum, the theoretical (Boldor et al., 2005) and measured temperature values start decreasing as the peanuts continue through the waveguide. This temperature reduction was caused mainly by convection (Boldor et al., 2005), but also by radiative and evaporative cooling, not accounted for in the ideal system. Radiative and convective cooling increase as pod temperature increases. The evaporative cooling also increases at higher temperatures (and power levels) as more water is evaporated.
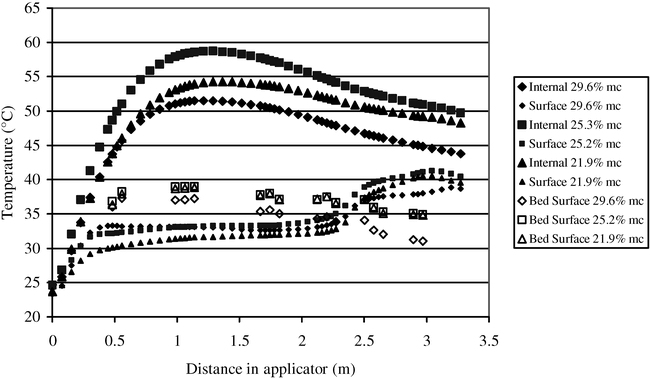
The external temperature profiles of the same pods of the runner-type peanuts (Fig. 3) show a different distribution when compared with the internal temperature profiles. The initial heat-up region (0–0.5 m) and the constant temperature drying region (0.5–2.0 m) are present for the surface of the pods. However, the surface temperature is much lower than the internal temperatures, and drying at constant temperature (second region) occurs much faster. This behavior is due to the different dielectric properties of the shells and the fact that the convective cooling has a greater effect on the surface of the pods.
Another major difference between the internal and surface temperatures as measured with the fiber optic probes is that on the surface, after the constant temperature drying region, the temperatures start increasing before settling to a new equilibrium value. There are two possible explanations for this effect. All the free water from the shells was removed and the shells will continue absorbing heat and experience an increase in temperature. At the second position of temperature equilibrium, water that was more tightly bound will start being vaporized, and the surface experiences a second constant temperature-drying region. A more plausible explanation is that in this region of the microwave curing chamber, the surface temperatures of the pods start to increase through conduction and radiation from the surrounding peanuts. While the infrared sensors measure the surface temperature of the whole peanut bed, the fiber optic probes were placed in the middle of the bed, where they were more affected by the heat coming from the surrounding peanut pods. The behavior of the temperature profiles at the pod surface in the middle of the peanut bed deserves further investigation.
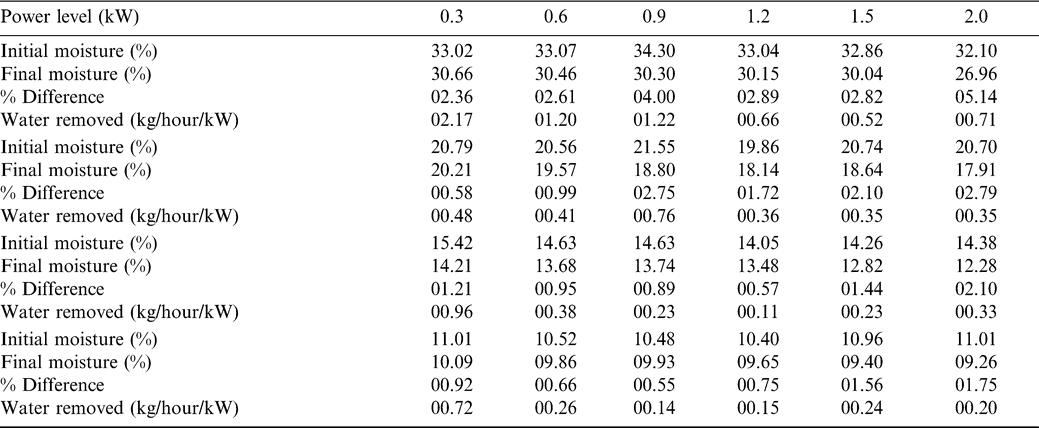
The reduction in MC for each of the three passes is more significant at higher MC and at the higher power level (Tables 1 and 2). Virginia-type peanuts (initially at 45.2% MC) exposed to microwave energy at 1.2 kW had a total reduction in MC to 33.2%, or an average of 4.0% reduction per pass. The same peanuts exposed to microwave energy at 2 kW had a reduction of 15.6%, or an average of 5.2% reduction per pass (Table 1).
Runner-type peanuts with an initial MC of 25.7% had a total reduction in MC to 17.4% at 1.2 kW, or an average of 2.8% per pass. At a power level of 2 kW, the MC was reduced from 24.6% to 15%, a total of 9.6% or an average of 3.2% per pass (Table 2).
The differences registered between the virginia-type peanuts and the runner-type peanuts are probably caused by the differences in MCs between the two types used in this study (45% initial MC for virginia-type, and 25% initial MC for runner-type).
Experimental Design 2
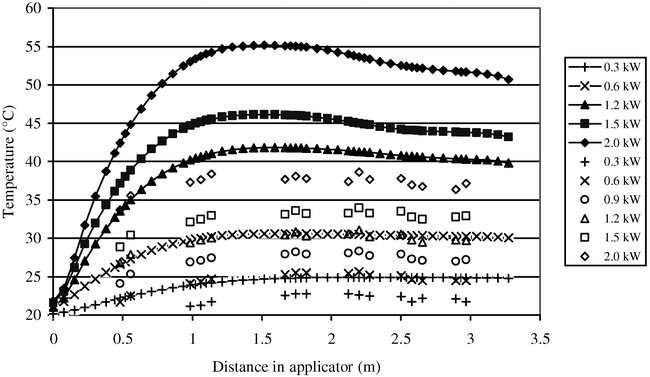
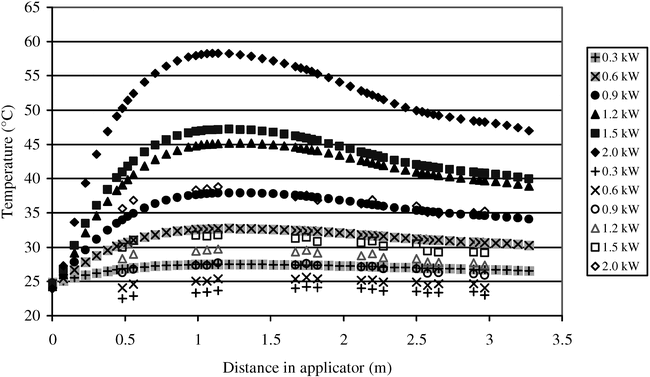
Examples of the temperature profiles of peanuts during microwave drying at the same initial MC and six power levels are shown in Fig. 4 and 5. At the same MC, the temperature profile was determined solely by the power level. The variability was higher for higher power levels, which was expected due to the higher temperatures registered at higher power levels (Boldor, 2003). Radiative, evaporative, and convective cooling were also observed in this experimental design. At the higher power levels, the higher kernel temperatures cause larger convective and radiative cooling, as well as more evaporative cooling.
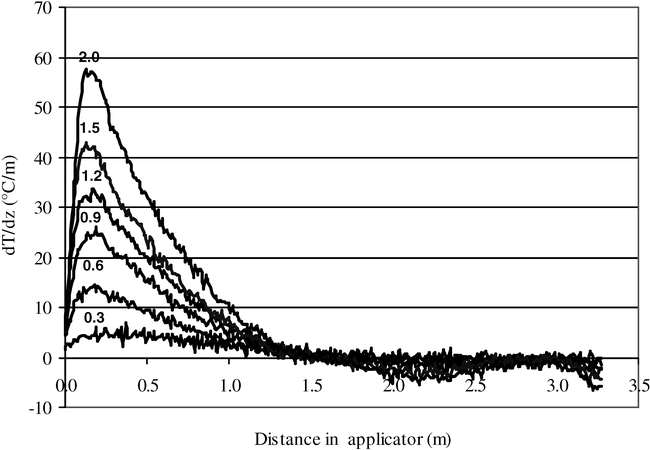
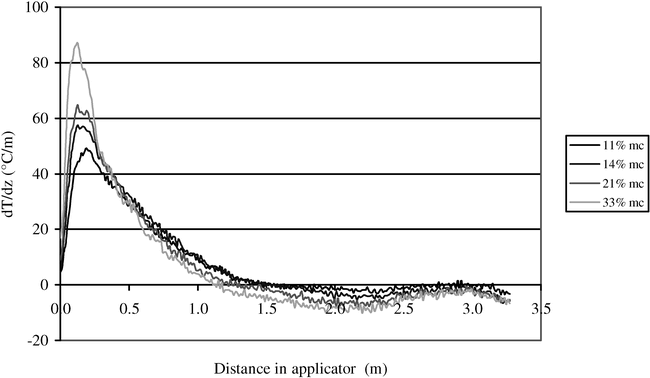
Plots of the first derivative of temperature versus distance (Fig. 6) show that the maximum temperature (derivative is zero) occurs at the same location for the same MC and is independent of the power level. The same is true for the maximum of the derivative (the maximum rate of temperature increase). These locations of the maximum temperature and of the maximum rate of temperature increase are important for process monitoring purposes.
The moisture loss at the six power levels for different initial MCs is presented in Table 3. In general, the higher power levels removed more moisture than the lower power levels, which is consistent with theoretical models previously developed (Boldor et al., 2005).
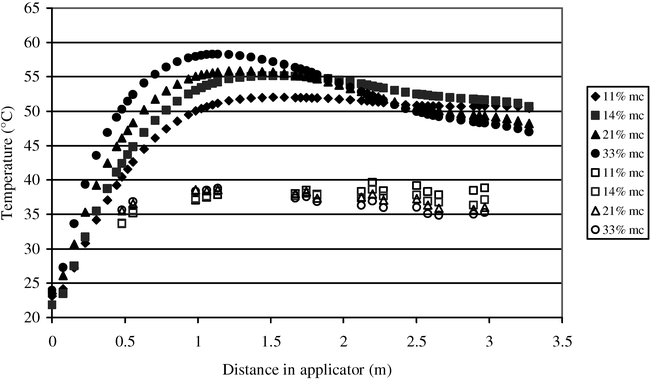
Plots of the temperature profiles at the same power level and the four different initial MCs tested are in Fig. 7. The variability in temperature profiles in general decreased with the MC (Boldor, 2003). The small difference between the maximum temperatures of the different MCs is due to the variability of dielectric properties with the MC (Equation [4]). This small difference can be considered negligible and confirms the fact that maximum temperatures depend mainly on the power level and the belt speed (Boldor et al., 2005).
However, there are two major differences between the temperature profiles at the same power level. For the constant temperature-drying region, the energy loss due to cooling is larger for the higher MCs at the same power level. With the assumption that the radiant emissivity of the peanuts is relatively constant at all MCs, radiative cooling can be neglected (Boldor et al., 2005). With the volumetric heating of the microwaves, the convective cooling at the surface of the peanuts depends only on the temperature and the surface area exposed to the air flow, which can be considered constants. These constants imply that the differences in the cooling process at the same power level are due to evaporative cooling. The higher the MC, the more water is being evaporated and the larger the cooling effect.
In the initial heat-up region, plots of the first derivative of temperatures with respect to distance (Fig. 8) show that the location of the maximum temperatures (where the derivative is zero) changes with the MC. As the MC decreases, the location of the maximum temperature moves further from the entrance to the microwave drying chamber. Even though the maximum temperature can be considered the same for the different MCs, the time (or distance in the waveguide) to get to that maximum temperature is longer as the MC decreases. The same observation is true for the location of the maximum rate of temperature increase (where the derivative is at maximum). This behavior is again consistent with theoretical models previously developed (Boldor et al., 2005). The higher the MC, the higher the attenuation factor (Boldor, 2003) and the faster the temperature increase.
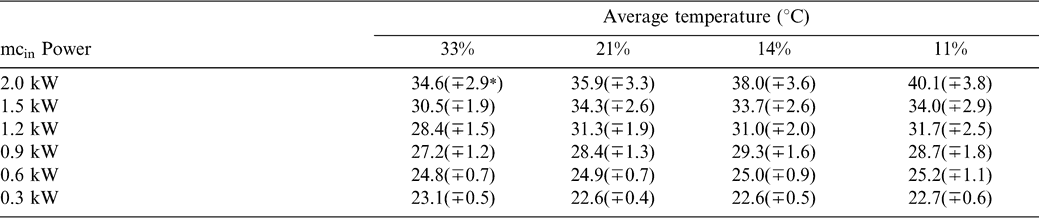
The distributions of the surface temperatures of peanuts defined within a rectangular region of the infrared image, taken at the exit of the microwave curing chamber for all MCs and power levels used in this experimental design, were very different (Fig. 9 and 10). The average temperatures and respective standard deviations of the regions are listed in Table 4. The average temperatures and standard deviations increased with increasing power level and also increased with a decrease in MC. This effect was more visible at the higher power levels than at the lower power levels. This response indicates that the drier the peanuts, the hotter their surface at the exit of the microwave applicator. While the surface temperatures at the beginning of the process increase proportionally with the MC, toward the end of the process the proportionality is reversed. A similar effect was observed on both the heat flux and the convective heat transfer coefficient during immersion frying in oil (Hubbard and Farkas, 2000). While at the beginning of the frying process both the heat flux and the convective heat transfer coefficients were proportional with the oil temperature, toward the end of the process the proportionality was reversed. Hubbard and Farkas (2000) explained this behavior through the different rates of drying that occur at the different oil temperatures and the total amount of water available for drying. Since the rate of drying in microwave is lower at lower initial MCs, less microwave energy is used as latent energy at lower MC, and is converted into sensible heat and raises the temperature of the peanut.
Conclusions
The internal and surface temperature distribution was determined for farmer stock peanuts undergoing drying in a traveling wave microwave applicator. The experimental results confirmed previous theoretical predictions (Boldor et al., 2005) that the temperature profiles were determined only by the power level at the same MC and only by the MC at the same power level. At the same MCs, the maximum temperatures and maximum rates of temperature increase occurred in the same time at the same location in the microwave applicator at all power levels tested. The negligible effect of temperature on the dielectric properties of the farmer stock peanuts confirmed previously performed measurements (Boldor et al., 2004). At the same power levels, the maximum temperatures were the same for all MCs tested, but the rate at which that maximum was reached increased with the increasing MCs. This result shows the dependence of the dielectric loss and the attenuation constant α on the MC of the peanuts, an effect that was also previously observed (Boldor, 2003). The measured moisture losses during microwave drying were also in line with previous theoretical estimations (Boldor, 2003) and the total moisture reduction in consecutive passes at the same power level was determined.
Literature Cited
ASAE Standards 2000 Moisture Measurement – Peanuts. ASAE S410.1 Dec. 97. American Society of Agricultural Engineers, 2950 Niles Road, St. Joseph, MI 49085-9659 USA
Baldwin J. A. and Beasley J. P. 1990 Peanuts – A grower's guide to quality Planters LifeSavers Co. Winston-Salem NC .
Baker K. D. , Cundiff J. S. , and Wright F. S. 1993 Peanut quality improvement through controlled curing. Peanut Sci 20 : 12 – 16 .
Beke J. , Mujumdar A. S. , and Bosisio R. G. 1995 Drying of fresh and rewetted shelled corn in microwave fields. Drying Tech 13 : 463 – 475 .
Beke J. , Mujumdar A. S. , and Giroux M. 1997 Some fundamental attributes of corn and potato drying in microwave fields. Drying Tech 15 : 539 – 554 .
Blankenship P. D. and Chew V. 1978 Reducing energy consumption during conventional drying. Proc. Amer. Peanut Res. Educ. Soc 10 : 45 – 49 .
Blankenship P. D. and Chew V. 1979 Peanut drying energy consumption. Peanut Sci 6 : 10 – 13 .
Boldor D. 2003 Temperature control of the continuous peanut drying process using microwave technology Ph.D. Thesis. North Carolina State Univ Raleigh 136 pp .
Boldor D. , Sanders T. H. , and Simunovic J. 2004 Dielectric Properties of In-Shell and Shelled Peanuts at Microwave Frequencies. Trans. ASAE 47 : 1159 – 1169 .
Boldor D. , Sanders T. H. , Swartzel K. R. , and Farkas B. E. 2005 A Model for Temperature and Moisture Distribution during Continuous Microwave Drying. Accepted for publication in Journal of Food Process Engineering
Bouraoui M. , Richard P. , and Durance T. 1994 Microwave and convective drying of potato slices. J. Food Proc. Eng 17 : 353 – 363 .
Boyes S. , Chevis P. , Holden J. , and Perera C. 1997 Microwave and water blanching of corn kernels: Control of uniformity of heating during microwave blanching. J. Food Proc. Preservation 21 : 461 – 484 .
Butts C. L. 1996 Comparison of peanut dryer control strategies. Peanut Sci 23 : 86 – 90 .
Chai L. and Young J. H. 1995 Simulated air flow rate effects on drying times and costs for conventional and recirculating peanut drying facilities. Peanut Sci 22 : 8 – 14 .
Clark D. E. , Sutton W. H. , and Lewis D. A. 1997 Microwave processing of materials. 61 – 96 In Clark D. E. , Sutton W. H. , and Lewis D. A. eds. Microwaves: Theory and application in materials processing IV The American Ceramic Society Westerville, OH .
Erle U. and Schubert H. 2001 Combined osmotic and microwave-vacuum dehydration of apples and strawberries. J. Food Eng 49 : 193 – 199 .
Funebo T. and Ohlsson T. 1999 Microwave assisted air dehydration of apple and mushroom. J. Food Eng 38 : 353 – 367 .
Funebo T. , Ahrné L. , Kidman S. , Langton M. , and Skjöldebrand C. 2000 Microwave heat treatment of apple before air dehydration – Effects on physical properties and microstructure. J. Food Eng 46 : 173 – 182 .
Goedeken D. L. , Tong C. H. , and Lentz R. R. 1991 Design and calibration of a continuous temperature measurement system in a microwave cavity by infrared imaging. J. Food Proc. Preservation 15 : 331 – 337 .
Griffiths D. J. 1999 Introduction to electrodynamics.3rd Ed Prentice-Hall Upper Saddle River, NJ 364 – 415 .
Hubbard L. J. and Farkas B. E. 2000 Influence of oil temperature on convective heat transfer during immersion frying. J. Food Proc. Preservation 24 : 143 – 162 .
Jones P. L. 1975 RF paper drying - Its theory and practice. Paper Tech and Ind June : 187 – 193 .
Jones P. L. 1986 High frequency dielectric heating in paper making. Drying Tech 4 : 217 – 244 .
Katz T. A. 2002 The effect of microwave energy on roast quality of microwave blanched peanuts Masters Thesis. North Carolina State Univ Raleigh 107 pp .
Lu L. , Tang J. , and Ran X. 1999 Temperature and moisture changes during microwave drying of sliced food. Drying Tech 17 : 413 – 432 .
Maskan M. 2000 Microwave/air and microwave finish drying of banana. J. Food Eng 44 : 71 – 78 .
Metaxa A. C. and Meredith R. J. 1983 Industrial microwave heating Peter Peregrinus Ltd London, UK 357 pp .
Mullin J. and Bows J. 1993 Temperature measurement during microwave cooking. Food Additives and Contaminants 10 : 663 – 672 .
Nelson S. O. 1973 Electrical properties of agricultural products (A Critical Review). Trans. ASAE 16 : 384 – 400 .
Ponne C. T. , Baysal T. , and Yuksel D. 1994 Blanching leafy vegetables with electromagnetic energy. J. Food Sci 59 : 1037 – 1041, 1059 .
Prabhanjan D. G. , Ramaswamy H. S. , and Raghavan G. S. V. 1995 Microwave-assisted convective air drying of thin layer carrots. J. Food Eng 25 : 283 – 293 .
Ptasznik W. , Zygmunt S. , and Kudra T. 1990 Simulation of RF-assisted convective drying for seed quality broad bean. Drying Tech 8 : 977 – 992 .
Rausch T. D. 2002 Effect of microwave energy on blanchability and shelf-life of peanuts Masters Thesis. North Carolina State Univ Raleigh 102 pp .
Rogers R. A. and Brusewitz G. H. 1977 Drying spanish peanut pods with short duration, high temperature air cycled daily. Peanut Sci 4 : 12 – 15 .
Rosenthal I. 1992 Electromagnetic radiation in food science Springer-Verlag Berlin 244 pp .
Roussy G. and Pearce J. A. 1995 Foundations and Industrial Applications of Microwave and Radio Frequency Fields: Physical and Chemical Processes J. Wiley and Sons New York, NY 371 – 444 .
Sanga E. , Mujumdar A. S. , and Raghavan G. S. V. 2000 Experimental results of combined microwave-convection drying of non-homogeneous (composite) materials Presented at the 2000 ASAE Annual International Meeting, Paper No. 006099. ASAE, 2950 Niles Rd., St. Joseph, MI 49085–9659.
Schiffmann R. F. 1997 Principles of industrial microwave and RF heating. 41 – 60 In Clark D. E. , Sutton W. H. , and Lewis D. A. eds. Microwaves: Theory and Application in Materials Processing IV The American Ceramic Society Westerville, OH .
Shivhare U. , Raghavan G. , and Bosisio R. 1991 Drying of corn using variable microwave power with a surface wave applicator. J. Microwave Power and Electromagnetic Energy 26 : 38 – 44 .
Stuchly S. S. and Hamid M. A. K. 1972 Physical parameters and microwave heating processes. J. Microwave Power and Electromagnetic Energy 7 : 117 – 137 .
Troeger J. M. 1982 Peanut drying energy consumption – A simulation analysis. Peanut Sci 9 : 40 – 44 .
von Hippel A. R. 1954 Dielectric materials and applications. The Technology Press of M.I.T., John Wiley Sons, Inc New York, NY Chapman Hall, Ltd London, UK 3 – 46 .
Young J. H. , Person N. K. , Donald J. O. , and Mayfield W. D. 1982 Harvesting, curing, and energy utilization. In Pattee H. E. and Young C. T. eds. Peanut Science and Technology Amer. Peanut Res. Educ. Soc., Inc Yoakum, TX .
Notes
- 1The research reported in this publication was a cooperative effort of the Agric. Res. Serv. of the USDA and the North Carolina Agric. Res. Serv., Raleigh, NC 27695-7643. Use of trade names in this publication does not imply endorsement by the USDA or the North Carolina Agric. Res. Serv. of the products named; nor criticism of similar ones not mentioned. [^]
- 2Dept. of Biological Agricultural Engineering, Louisiana State Univ., Baton Rouge, LA 70803 [^]
- 3USDA, ARS, Market Quality and Handling Res. Unit, North Carolina State Univ., Raleigh, NC 27695-7624; (919) 515-6312; Fax (919) 515-7124 [^]
- 4Dept. of Food Science, North Carolina State Univ., Raleigh, NC 27695-7624 [^] *Corresponding author (e-mail: tim_sanders@ncsu.edu