Introduction
Individual peanut seed can develop an objectionable off-flavor if exposed to certain environmental conditions. Typically, high moisture, immature peanuts exposed to temperatures above 35°C will produce a fruity-fermented (FF) off-flavor (Sanders et al., 1989a,b; Sanders et al., 1990). The intensity of FF off-flavor appears to be directly proportional to temperature, immaturity, and kernel moisture content (Whitaker and Dickens, 1964). High temperature exposure can occur in the windrow when peanuts are exposed to direct radiation from the sun or during curing when artificial heat is added to the drying air. When peanuts are exposed to these conditions, the assumption can be made that within each bulk lot of shelled peanuts, there exists a FF distribution among individual peanuts. Probably, a large percentage of peanuts in a bulk lot have no measurable FF off-flavor intensity and the remaining small percentage of peanuts have varying intensities of the FF off-flavor. If all peanuts in a lot were subjected to the same temperature, then the FF distribution among individual peanuts may be closely related to the maturity distribution among individual peanuts in the lot (Sanders, 1990; Sanders and Bett, 1995).
Currently, the peanut industry estimates the mean level of the FF attribute among all peanuts in a bulk lot by taking a 300 g sample of peanuts from the bulk lot. The test sample is roasted, blanched, and ground into a paste, a subsample of paste is removed from the comminuted test sample, and each member of a trained flavor panel scores the FF intensity. Each panel member is highly trained and experienced in evaluating peanut flavor as described by the peanut flavor lexicon (Johnsen et al., 1988; Sanders, et al., 1989b). Each panel member evaluates the intensity of the peanut flavor descriptors using standard, published sensory analysis procedures. All panel member scores are averaged and the average score is the best estimate of the true FF off-flavor intensity among all peanuts in the lot.
Customers who buy U.S. peanuts may specify in their purchase contract that the peanuts must have an average FF intensity below some threshold (Greene et al., 2006a; personal communication J. Leek and Associates, 2006). Occasionally, separate samples taken from the same lot by the seller and buyer will not agree when scored by their respective trained flavor panels. If a customer receives a lot that tests greater than a specified threshold, an economic hardship is created for both the buyer and seller of the lot. The lack of agreement in the FF off-flavor score is probably due to the uncertainty associated with the test procedure used by the seller and buyer of the peanuts to measure the FF intensity of peanuts in the bulk lot.
The test procedure used to estimate the FF intensity in a bulk lot consists of sampling, sample preparation, and measurement steps. Each step contributes to the overall uncertainty associated with the test procedure. Because of the uncertainty of the FF test procedure, it is not possible to determine with 100% certainty the true average FF intensity among all peanuts in the bulk lot by measuring the average FF intensity of peanuts in a sample taken from the lot.
Because of the uncertainty associated with sampling, sample preparation, and measurement steps, lots can be misclassified by a sampling plan. There is some chance that good lots (true FF intensity is below a defined tolerance) will test bad by the sampling plan (seller's risk) and some chance that bad lots (true average FF intensity is above a defined tolerance) will test good (buyer's risk) by the sampling plan. The performance (number of lots miss-classified or the buyer's and seller's risks) of a specific sampling plan can be predicted if the variability associated with sampling and measurement steps of the test procedure can be determined and if the FF distribution among replicated sample test results can be described.
The objectives of this study were to: (1) measure the total variability associated with the test procedure used to measure the FF intensity in peanuts, (2) partition the total variability associated with the FF test procedure into sampling, sample preparation, and measurement variance components, (3) measure the FF distribution among replicated samples taken from a bulk lot, and (4) demonstrate how to make best use of resources to reduce the uncertainty of the FF test procedure.
Materials and Methods
Theoretical Considerations
It was assumed that the total variability, (s2 t) associated with the test procedure to estimate the FF intensity of peanuts in a bulk lot is the sum of the sampling (s2 s), sample preparation (s2 sp), and measurement (s2 m) variances (Whitaker et al., 1974).
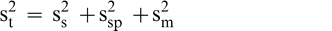 (1)
(1)
Sampling error occurs because the FF distribution among individual peanuts causes differences among replicated sample test results taken from the same lot. Once a sample is prepared (roasted, blanched, and ground), the FF intensity may differ among replicated subsamples of paste taken from the same comminuted sample (sample preparation error). Finally, evaluation of the FF intensity may differ among individual sensory panel members when tasting peanuts from the same sample (measurement error). It was assumed that the sample preparation error is negligible (s2 sp = 0) since all peanuts in the sample are ground into a homogenous paste and the FF intensity will not differ among replicated subsamples taken from the same comminuted test sample.
Experimental Design
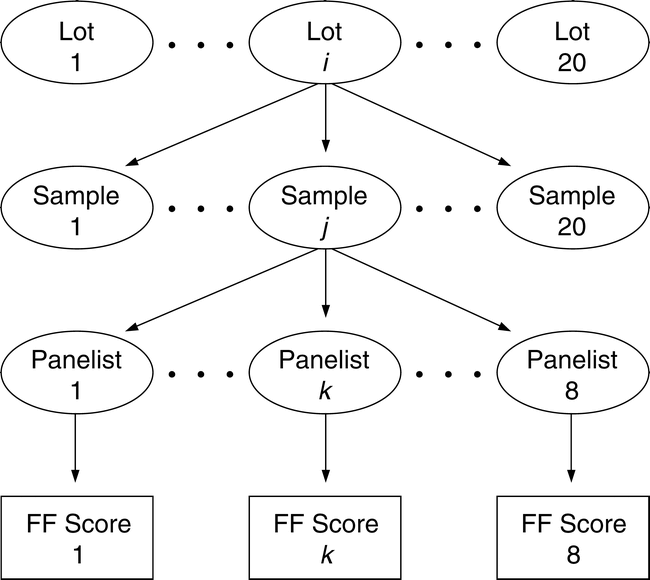
To measure the sampling and measurement variability and the FF distribution among sample test results, a balanced nested design was developed (Figure 1). Twenty bulk lots of medium runner type peanuts were identified by commercial testing as having FF off-flavor intensity ranging from 0.0 (no FF off flavor) to 4.0. A 5 kg bulk sample was removed from each identified lot. Using a riffle divider, 20 samples of 250 g each were removed from the 5 kg bulk sample. Using standard industry procedures (Greene, J.L. et al. 2006b), each 250 g sample was roasted, blanched, and ground into a paste. Each member of a highly trained descriptive sensory panel rated the FF intensity in a subsample taken from the ground 250 kg sample. Depending on the availability of panel members, each ground sample was usually rated by the same 8 panel members. All panelists used the SpectrumTM method to evaluate the intensity of all terms in the peanut lexicon (Johnson et al., 1988; Sanders et al., 1989b). Approximately 20×20×8 or 3200 FF scores, identified by panel member, sample number, and lot number, were recorded in the database for statistical analysis.
Statistical Analysis
Using Proc Mixed in SAS, an estimate of the total, sampling, and measurement variances was determined for each lot. The average FF intensity among the 160 FF off-flavor scores (8 panel member scores per sample time 20 samples per lot) was also determined for each lot. The 20 sampling and measurement variance estimates were plotted versus the average FF intensity for each lot to determine if each variance component was a function of the FF intensity.
Observed Distribution
An observed FF distribution among the 20 sample test results for was constructed for each lot. A total of 20 observed distributions, one for each lot, were constructed. The observed cumulative FF distribution for a given lot was constructed by ranking the 20-FF sample test results from high to low. The highest FF value was assigned a cumulative probability of 1.0. The next to highest FF value was assigned a cumulative probability of 1.0 – 1/20 or 0.95. The cumulative probability associated with each smaller FF value was reduced by 1/20 or 0.05. The cumulative probability associated with the smallest FF value was assigned a probability of 1/20 or 0.05.
Theoretical Distribution
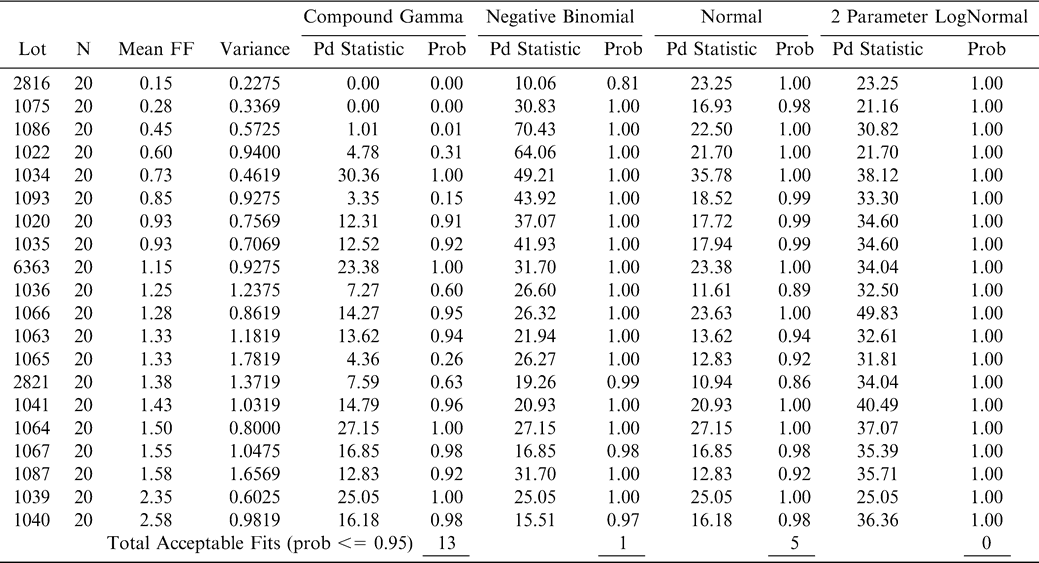
Four theoretical distributions, normal, lognormal, negative binomial, and compound gamma were chosen as possible models to simulate the observed FF distribution among the 20 sample test results taken from a lot (Giesbrecht and Whitaker, 1998). These four theoretical distributions were chosen to give a broad descriptive range of distributional shapes from symmetrical (normal) to highly skewed (negative binomial) distributional shapes. Each theoretical distribution was compared to each observed FF distribution for a total of 80 comparisons.
Parameter Estimation Methods
The predicted FF distribution among sample test results was calculated from a theoretical distribution using distribution parameters computed from the mean and variance among the 20-FF sample test results. Parameters of the four theoretical distributions were estimated using the method of moments (Giesbrecht and Whitaker, 1998). The method of moments provides a direct and uncomplicated method of estimating the parameters of each theoretical distribution. Parameters of each theoretical distribution are estimated directly from the measured mean, I, and variance, S2 t, among the 20-FF sample test results associated with each lot (Giesbrecht and Whitaker, 1998; Whitaker et al., 1972).
Goodness of Fit
The Power Divergence (PD) test statistic, which is a conservative modification of the Chi Square GOF test, was selected as the criterion to evaluate the goodness of fit (GOF) between the theoretical and observed distributions (Read and Cressie, 1988). For a given lot, the range among the 20 sample test results is divided into 10 intervals of equal width and the number of sample test results that fell into each interval was counted. The expected number of sample test results in each interval is 2 (20 sample test results divided by 10 intervals). The PD statistics were calculated using Equation 1 and compares the observed number of sample test results in each interval to the expected number or 2.
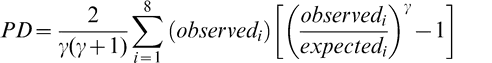 (1)
(1)
Results
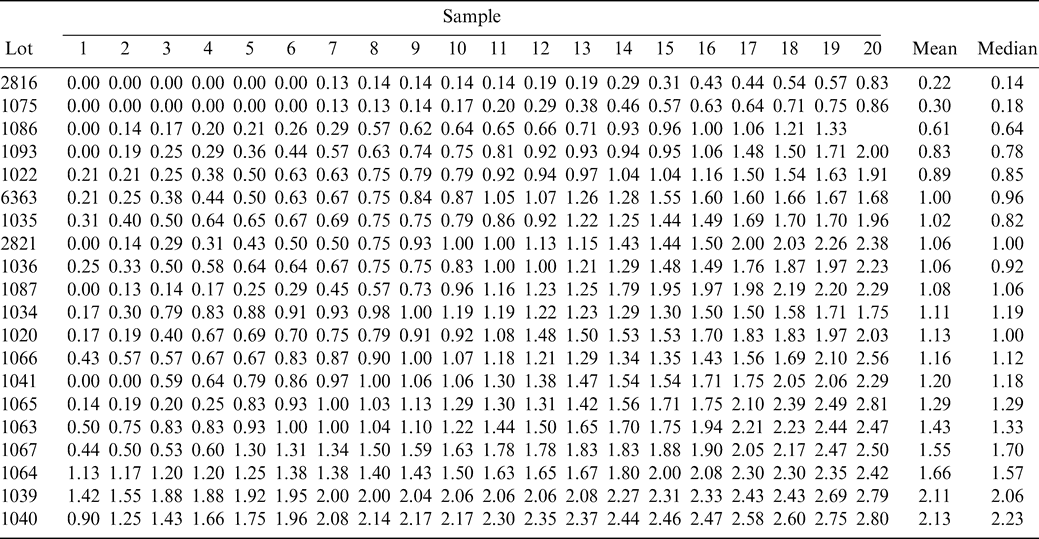
The FF intensity for each sample and for each lot is shown in Table 1. The FF intensity associated with each sample in Table 1 is the average of all eight-panel member scores. For each lot, sample intensities are ranked from low to high to more easily view the range among sample test results within each lot. The best estimate of the true FF intensity of a lot is the average of the 160 FF scores (20 samples × 8 panel scores per sample). The average FF intensity among the 20 lots varied from 0.2 to 2.1.
Variance
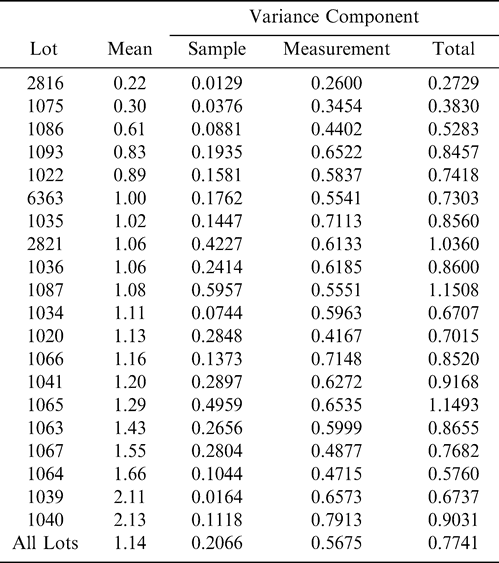
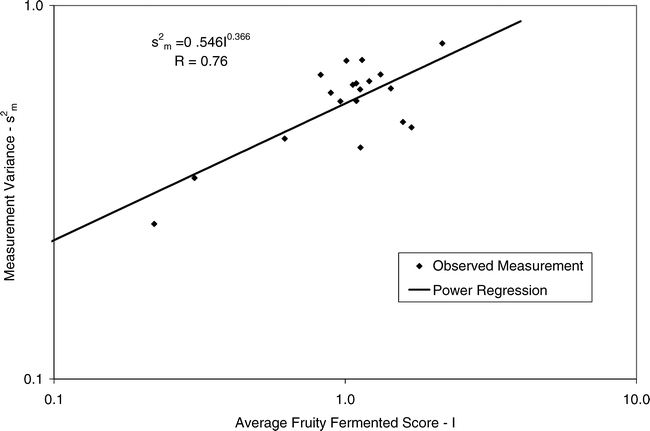
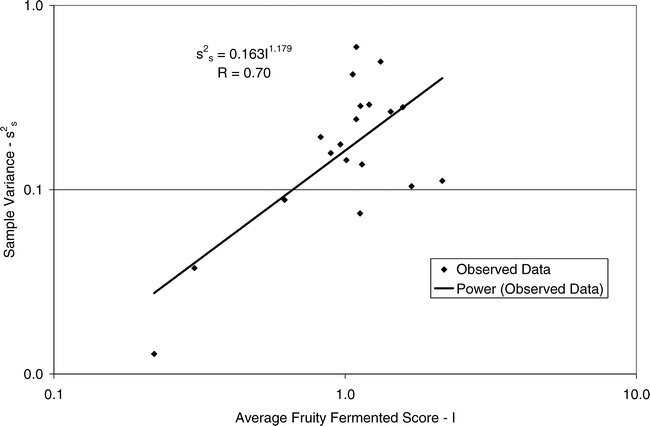
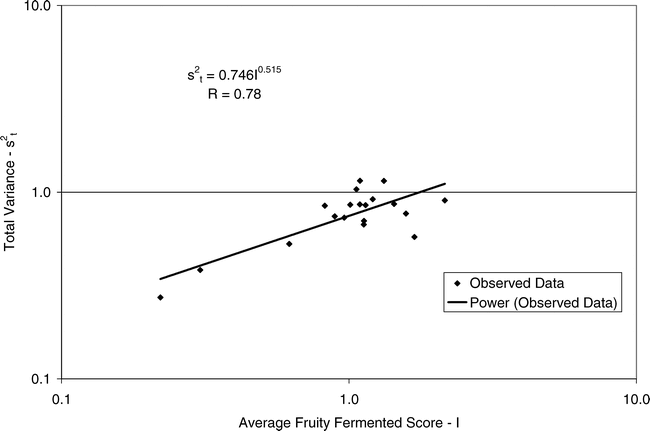
Using Proc Mixed in SAS, the mean FF intensity, total variance, sampling variance, and measurement variance for each lot is shown in Table 2. A full log plot (sometimes called a log-log plot) of the measurement variance, sampling variance, and total variance versus the average FF intensity (Table 2) is shown in Figures 2, 3, and 4, respectively. The functional relationship between variance (s2) and FF intensity (I) was determined using a linear regression analysis on the log values. The regression results are also shown in each figure along with the measured variances. The regression equations for measurement, sampling, and total variances as a function of the FF intensity are shown in Equations 2, 3, and 4, respectively.
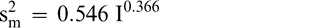 (2)
(2)
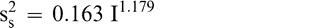 (3)
(3)
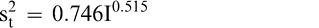 (4)
(4)
Unfortunately, the range in FF intensity among the 20 lots was not as wide as hoped. There was a clumping of mean and variance point in Figures 2, 3, and 4 and as a result the slope of the regression equations (slope in the log scale is the exponent on the I term in equations 2, 3, and 4) was determined with only 3 to 4 points. The attempt to sample peanut lots over a wide range of FF scores proved to be very difficult.
The measurement, sampling, and total variances can be predicted from Equations 2, 3, and 4, respectively, for a given FF intensity, I. For example, when measuring a lot with a true FF intensity (I) of 2.0, the measurement and sampling variances among individual panel members and among 250 g test samples are 0.704 and 0.369, respectively. The total variance of 1.073 was determined by adding the measurement and sampling variances together instead of using Equation 4. At a FF intensity of 2.0, measurement error accounts for 65.6% (0.704/1.073) of the total error and sampling error accounts for 34.4% (0.369/1.073) of the total error.
Reducing Uncertainty
The measurement variance in Equation 2 reflects the variability among individual panel member scores and is specific to the particular sensory panel members used in this study. The measurement variance can be reduced by averaging the scores of 2 or more panel members. Equation 2 can be modified to predict the measurement variance associated with averaging any number of panel members (np).
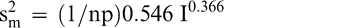 (5)
(5)
Because the uncertainty associated with other sensory panels was not determined, the measurement variance in Equations 2 and 5 may be more or less than the uncertainty associated with other sensory panels. However, highly trained sensory panels that use the SpectrumTM method should have similar levels of uncertainty.
The sampling variance in Equation 3 is specific to a 250 g sample size. Increasing the size of the test sample taken from the lot can reduce the sampling variance. Equation 3 can be modified to reflect the sampling variance associated with any sample size ns in grams.
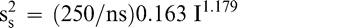 (6)
(6)
The total variance associated with a FF test procedure that averages np panel member scores when using a test sample of size ns is obtained by adding Equations 5 and 6.
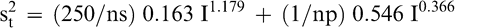 (7)
(7)
As an example, the uncertainty associated with the FF test procedure used by the peanut industry to estimate the intensity of the FF off-flavor in a bulk lot can be estimated using Equation 7. The peanut industry currently uses a 300 g sample and averages the scores of 5 panel members. The measurement, sampling, and total variances associated with the current industry FF test procedure (np=5 panel members and ns=300 g) when testing a lot with a true FF intensity of 2.0 is estimated from Equations 5, 6, and 7 to be 0.141, 0.308, and 0.449, respectively. The coefficient of variation (CV) associated with measurement, sampling, and total variances are 18.8, 27.7, and 33.5%, respectively. For this example, measurement error accounted for 31.4% (0.141/0.449) of the total error and sampling accounted for 68.6% (0.308/0.449) of the total error. The measurement CV of 18.8% would appear to a reasonable level of uncertainty when comparing the ability of human taste buds to highly precise analytical equipment such as high performance liquid chromatography, which has levels of uncertainty of about 5 to 10% (Whitaker et al., 1974).
In addition, the total variance of 0.449 can be used to predict the range of sample test result one would expect when sampling a lot with a FF intensity of 2.0 using the standard peanut industry FF test procedure (ns=300 g and np=average of 5 panelists). Assuming a normal distribution and 95% confidence limits, the FF intensity among samples would range from [2.0 +/− (1.96 (sqrt (0.449))] or range from [2.0 +/− 1.31] or range from 0.69 to 3.31. The major source of uncertainty associated with the peanut industry FF test procedure is associated with the 300 g sample size (68.6% of the total uncertainty). Further reduction in the uncertainty associated with the industry FF test procedure can be achieved by increasing sample size above 300 g. For example, the measurement, sampling, and total variances associated with the FF test procedure that quantified the FF intensity in a 600 g sample by averaging 5 panel member scores are 0.141, 0.154, and 0.295, respectively (For I = 2.0 in Equation 7). For this example, the measurement and sampling uncertainty are about the same magnitude.
Distribution among Sample Score
In the above example that predicted the range among sample test results when sampling a lot with a FF intensity of 2.0 and using the standard industry FF test procedure (ns=300 g and np=5 panelists), the FF distribution among sample test results was assumed to be normally distributed. However, as reported by Greene et al. (2006b), the FF distribution among the 20-sample test results for a single panel member appears to be skewed, especially for lots with low FF intensity values. The median is less than the mean for 15 of the 20 lots (Table 1) indicating that the distribution among the test results is positively skewed and not symmetrical such as the normal distribution.
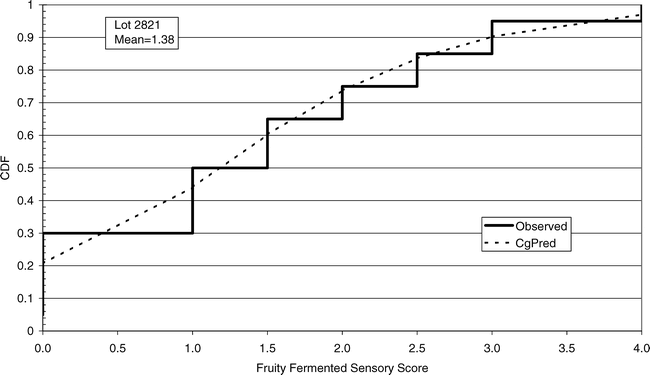
Using FF intensity scores associated with one panel member (identified as panel member A), an observed cumulative FF distribution among the 20 sample test results was constructed for each lot (reflecting the uncertainty associated with Equation 7 where ns = 250 g and np =1 panel member). The 20 observed FF distributions were each compared to the normal, lognormal, negative binomial, and compound gamma theoretical distributions (Giesbrecht and Whitaker, 1998). Using the method of moments, the mean and variance values computed from panel member A's FF scores for each lot were used to calculate parameters for each of the four theoretical distributions (Read and Cressie, 1988). A suitable fit occurred when the probability associated with the fit statistic was 0.95 or less. Goodness of fit tests (Table 3) indicated that the compound gamma provided the highest number of suitable fits to each of the 20 FF distributions. An example of the observed and theoretical distributions for lot 2821 is shown in Figure 5.
Cumulative observed (solid line) and predicted (dashed line) FF distributions (CDF) among FF intensity values for panelist A from lot 2821. The predicted cumulative FF distribution was calculated using the compound gamma distribution with mean and variance parameters shown in Table 3 for lot 2821.
The distribution among sample test results can be predicted for specified sample size (ns) and use of a specified number of panel members (np) using variance Equation 7 and the compound gamma distribution. In future studies, a model will be developed using the compound gamma distribution and variance Equation 7 to predict the probability of accepting a lot with a given FF intensity using a given FF test procedure.
Summary and Conclusions
This study indicated that the measurement, sampling, and total variances associated with the standard industry test procedure (300 g sample and average of 5 panels member scores) used to score a bulk lot with a true FF score of 2.0 were predicted to be 0.141, 0.308, and 0.449, respectively. For this example, measurement error accounted for 31.4% (0.141/0.449) of the total error and sampling accounted for 68.6% (0.308/0.449) of the total error. Since there is a different cost associated with reducing sampling and measurement uncertainty, the best use of resources to reduce the total variability associated with estimating the true FF off-flavor of a bulk lot may be to increase sample size. The variance and distributional information among sample test results will be used to develop a model to predict the performance of FF sampling plans for peanuts. With the evaluation model, the effect of sample size and the number of panels member used to evaluate the FF intensity in a sample on the chances of accepting bad lots (buyer's risk) and the chances of rejecting good lots (seller's risk) can be determined. Sampling plan design parameters such as sample size and number of panel members used to evaluate the FF intensity in bulk peanut lots can be investigated so that sampling plans developed for the peanut industry will not exceed specified risk levels.
Literature Cited
Giesbrecht F. G. and Whitaker T. B. 1998 Investigations of the problems of assessing aflatoxin levels in peanuts. Biometrics 54 : 739 – 753 .
Greene J. L. , Bratka K. J. , Drake M. A. , and Sanders T. H. 2006a Effectiveness of category and line scales to characterize consumer perception of fruity fermented flavor in peanuts. J. Sensory Studies 21 : 146 – 154 .
Greene J. L. , Whitaker T. B. , Hendrix K. W. , and Sanders T. H. 2006b Fruity Fermented Off-flavor Distribution in Samples from Large Peanut Lots. J. Sensory Studies accepted for publication, October 2006.
Johnsen P. B. , Civille G. V. , Verercellotti J. R. , Sanders T. H. , and Dus C. A. 1988 Development of a lexicon for the description of peanut flavor. J. Sensory Studies 3 : 9 – 17 .
Read T. R. C. and Cressie N. A. C. 1988 Goodness-of-Fit Statistics for Discrete Multivariant Data New York, NY Springer-Verlag .
Sanders T. H. 1990 Maturity distribution in commercial sized florunner peanuts. Peanut Sci 16 : 91 – 95 .
Sanders T. H. and Bett K. L. 1995 Effect of harvest date on maturity, maturity distribution, and flavor of florunner peanuts. Peanut Sci 22 : 124 – 129 .
Sanders T. H. , Blankenship P. D. , Vercellotti J. R. , and Crippen K. L. 1990 Interaction of curing temperatures and inherent maturity distribution on descriptive flavor of commercial grade sizes of florunner peanuts. Peanut Sci 17 : 85 – 89 .
Sanders T. H. , Vercellotti J. R. , Blakenship P. D. , Crippen K. L. , and Civille G. V. 1989b Interaction of maturity and curing temperature on descriptive flavor of peanuts. J Food Sci. 54 : 1066 – 1069 .
Sanders T. H. , Vercellotti J. R. , Crippen K. L. , and Civille G. V. 1989a Effect of maturity on roast color and descriptive flavor of peanuts. J Food Sci. 54 : 475 – 477 .
Whitaker T. B. and Dickens J. W. 1964 The effects of curing on respiration and off-flavor in peanuts. Proc Auburn, AL Third National Peanut Research Conference 71–80 .
Whitaker T. B. , Dickens J. W. , and Bowen H. D. 1974 Effects of curing on the internal oxygen concentration of peanuts. Trans. ASAE 17 : 567 – 569 .
Whitaker T. B. , Dickens J. W. , and Monroe R. J. 1974 Variability of aflatoxin test results. J. American Oil Chemists' Soc 51 : 214 – 218 .
Whitaker T. B. , Dickens J. W. , Monroe R. J. , and Wiser E. H. 1972 Comparison of the observed distribution of aflatoxin in shelled peanuts to the negative binomial distribution. J. American Oil Chemists' Soc 49 : 590 – 593 .
Notes
- The use of trade names in this publication does not imply endorsement by the USDA or the N.C. Agricultural Research Service of the products named nor criticism of similar ones not mentioned. [^]
- U.S. Department of Agriculture, Agricultural Research Service, Box 7625, N.C. State University, Raleigh, NC, 27695-7625 [^]
- Biological and Agricultural Engineering Department, Box 7625, N.C. State University, Raleigh, NC, 27695-7625 [^]
- Food Science Department, Box 7624, N.C. State University, Raleigh, NC, 27695-7624 [^]
- U.S. Department of Agriculture, Agricultural Research Service, Box 7624, N.C. State University, Raleigh, NC, 27695-7624 [^]
- Corresponding Author: (email: Tom_Whitaker@ncsu.edu) [^]
Disclaimer
Author Affiliations